かんとこうブログ
2020.04.06
外出自粛の効果は?
昨日の朝日新聞に、グーグルが公表した世界各国の人の移動の増減データが掲載されていました。これは、スマホの位置情報提供に同意している利用者のデータを使用して、1月3日~2月6日までのデータに対し、3月末ごろのデータと比較し、「小売店や娯楽施設(飲食店含む)」、「職場」、「住宅」など6種類の場所への人の移動の増減割合をグーグルが公表したもので、日本については、都道府県別のデータが示されています。今日はこの増減データをもとに感染者数に与える影響を考えてみます。
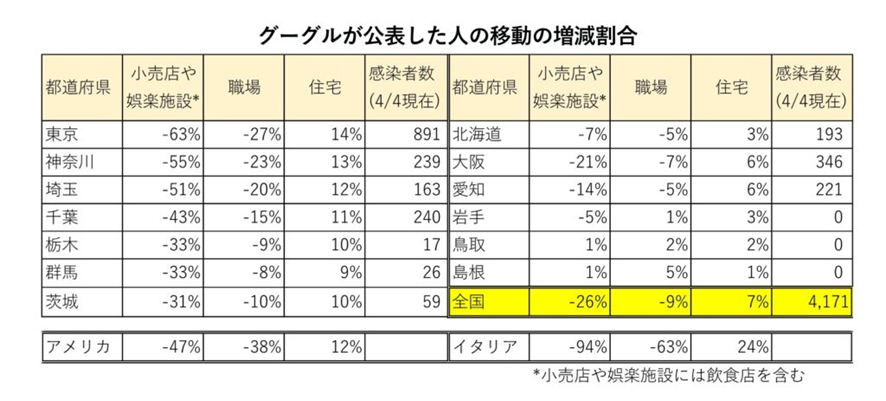
最も顕著な増減があったのは東京で、「小売店・娯楽」が63%減少、「職場」が27%減少、「住宅」14%増加でした。最も増減が少なかった県はいまだに感染者の出ていない県であり、ほとんど増減がありませんでした。やはり東京はじめ大都市周辺の増減が大きいことが明らかです。全国では、「小売店・娯楽」が26%減少、「職場」が9%減少、「住宅」7%増加となりましたが、この数値は、感染拡大が進み厳しい外出禁止令が出されているアメリカやイタリアに比べてはるかに小さな値でした。強制力のない要請段階ですのである意味仕方ないことかもしれませんが、果たしてこのような数値で果たして感染を抑制できるのでしょうか?
外出抑制率と感染者増加について正確なシミュレーションを行うことは、さすがに手に余ることでできませんが、基本となる考え方からおおよその推測くらいはできそうだとわかりました。感染病流行のシミュレーションは、SIRモデルと呼ばれる数理モデルを用いて計算されます。SIRとは、集団を構成する三つの群、S:未感染者(Susceptible)、I:感染者(Infected)、R:感染後死亡もしくは回復したもの(Recovered)の頭文字をとったものです。これら3つの集団の構成人数を、接触あたりの感染率、回復率、などの数値を与えてシミュレーションする方法で、実際の感染症における感染者数に挙動に合致することが証明されています。
細かい説明は省きますが、ポイントが、感染率βは以下の式で計算されるということです。β=m*p/Nで計算されます。ここでmは接触者数、pは感染係数、Nは集団の全体数です。つまり感染率は接触者数に比例するということです。言い換えると感染者数の増加割合はひとりひとりが接触する人数に依存するということです。
このSIRモデルについては、下のサイトを引用して書いていますが、このサイトでは簡単なシミュレーションをして、実際の感染者数がどのように変動するか解説しています。それによれば、1人1日あたりの接触者数が10人の場合と5人の場合とで、感染者の推移は驚くべき差がでています。(右の表:総人口は1000万人で試算)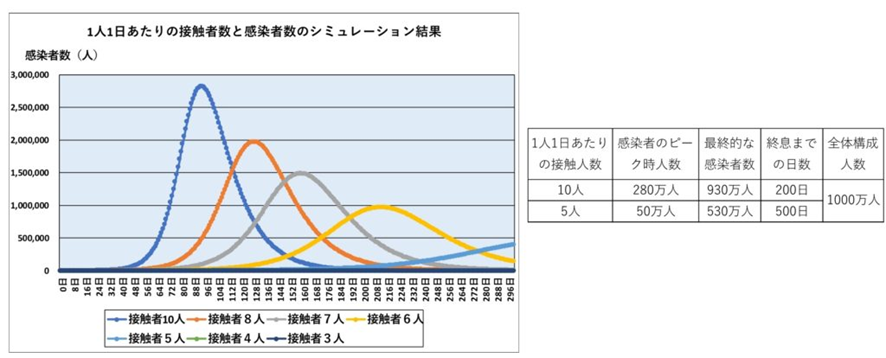
 このサイトでは10人と5人の場合しか計算していなかったので、接触者数を10人の場合から順に減らしていって、どう変化するか計算してみました。そのグラフが左の図ですが、ピーク時の感染者数は接触者の数にほぼ比例しています。またこのモデルでは接触者数が4人以下では、感染増加が起きずピークも現れないことがわかりました。このことはひとりひとりが接触者数を今の4割以下に減少させれば感染増加を防止できることになります。感染爆発を避けるためには接触者数の半減ではまだ足りないのです。
このサイトでは10人と5人の場合しか計算していなかったので、接触者数を10人の場合から順に減らしていって、どう変化するか計算してみました。そのグラフが左の図ですが、ピーク時の感染者数は接触者の数にほぼ比例しています。またこのモデルでは接触者数が4人以下では、感染増加が起きずピークも現れないことがわかりました。このことはひとりひとりが接触者数を今の4割以下に減少させれば感染増加を防止できることになります。感染爆発を避けるためには接触者数の半減ではまだ足りないのです。
もう一度冒頭のグーグルの調査結果を見ると、東京、神奈川など首都圏では、「小売や娯楽」へ出かける人が半分以下に減少し外出自粛の要請の効果が出ているように思われます。しかし、「職場」についてはまだまだ半減とはいかないようです。すべての職場でテレワークが難しいことも事実ですが、こうしたシミュレーション結果に鑑みれば、「職場」においても感染をさけるための、できる限りの手段を講じることが感染拡大防止に必要があるものと思われます。
本項のSIRモデルについては以下のサイトの内容を引用、参照しています。