かんとこうブログ
2021.03.05
3月21日の東京都の新規感染者数を数学的に予想してみると・・
緊急事態宣言を2週間程度延長するということになりました。となると、気になるのは3月21日時点での新規感染者数がどのくらいになっているかということです。今日は2月1日以降3月4日までの新規感染者数(7日間の移動平均)の推移から数学的に、2週間延長後の3月21日時点での東京都の新規感染者数を予想してみます。
まずは、2月1日から3月4日までの東京都の新規感染者数の推移と、エクセルの近似式機能を用いた4種類の近似式とそのR2乗の値をご覧ください。グラフの青線は皆同じものですが、赤の点線で表した近似式によって、縦軸の数値範囲が少し違っています。
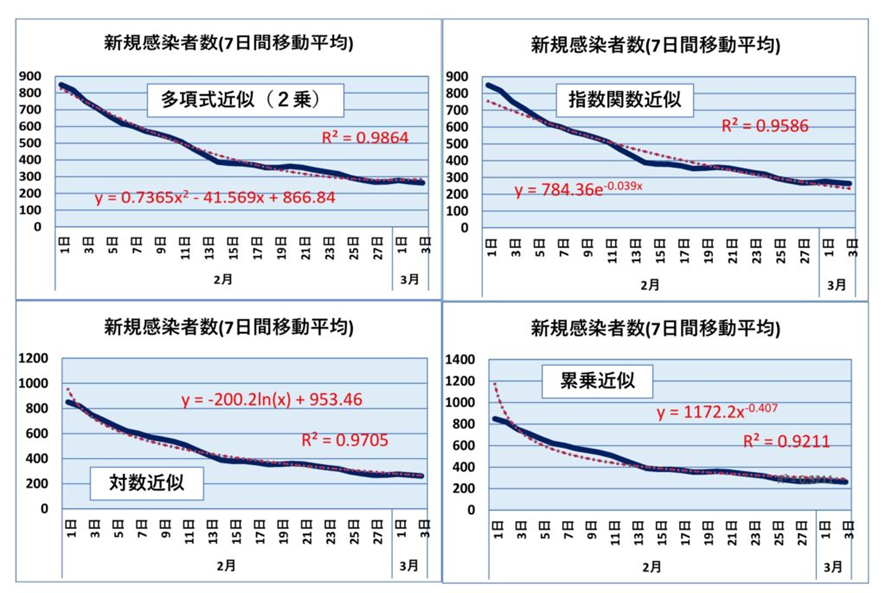
左上が多項式(2次式)近似、左下が対数近似、右上が指数関数近似、右下が累乗近似です。R2乗の数値は多項式が最も高くほぼ完ぺきな近似式になっています。直線近似では2月後半から3月にかけてのなだらかに裾野を引いた部分から大きく外れてしまいますが、一応計算だけはしてみました。その結果が下表です。
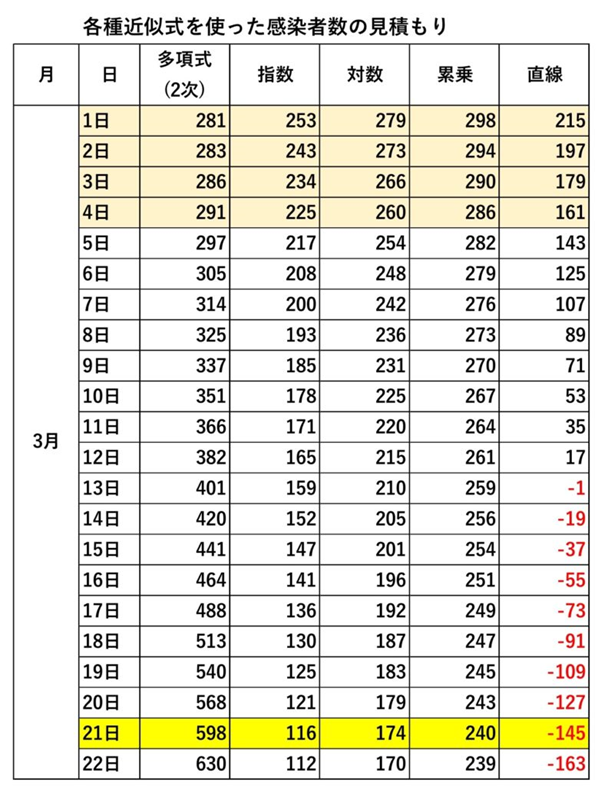
これはあくまで近似式の計算値であり、実際の感染者数とは異なりますが、3月はじめの実際の新規感染者数(7日間の移動平均)が270名前後であることから、この時点で、指数関数と直線近似は早くも実際の数値からはずれ始めていると言わざるを得ません。多項式(2次)、対数、累乗はまあ合格範囲と言えますので、ひとまずこの3つの式を使った場合の3月21日の新規感染者数の数字を予測値の候補としたいと思います。
ですが、このうち多項式(2次)には困った点があります。それは、正の係数をもった2次関数なので、次第に減少し極小値に到達したしたあとは増加に転じるということです。この近似式の極小値は2月28日でした。ということは3月1日以降は増加の一途ということになります。これは実際の推移とは一致していませんし、そうあってほしくもありません。残念ながら多項式も除外せざるを得ません。
となると残るのは対数と累乗になります。3月21日の東京都の新規感染者予測値は、対数近似が174人、累乗近似が240人となります。まとめると200人前後という表現になるでしょうか?
これはあくまで、数学的な近似の話であり、実際には人々の挙動が感染者数を決めます。ただ、政策的に大きな変化がないとすれば、そして人々の行動も変わらないとすれば、これまでの延長がどのような数値になるのかと予測するのはそれほど意味のないことでもないのかと思います。少しでもご参考になれば幸いです。